Математики получают новые фундаментальные результаты в функциональных неравенствах
Приглашенный профессор Университета RUDN Дурвудхан Сураган и команда коллег получили и установили новые типы функциональных неравенств. Неравенства Харди являются важным типом решения задач в математической физике. Результаты исследования были опубликованы в «Advances in Mathematics».
Свойства так называемых неравенств Харди изучались математиками во всем мире уже около века. Это отношения определенного типа для рядов и интегралов. Неравенства Харди изучаются в функциональном анализе и используются как вспомогательный инструмент во многих областях математики и механики, а также в теории вырожденных дифференциальных уравнений (в частных производных эллиптического типа), теории спектра, нелинейном анализе и теории интерполяции.
Большинство исследований, посвященных неравенствам Харди и их аналогам, выполняется в евклидовых векторных пространствах. С точки зрения высшей математики евклидово пространство представляет собой множество произвольных элементов, на которых задана операция точечного произведения. Двумерные и трехмерные пространства являются частными случаями евклидовых пространств. Команда из RUDN расширила теорию неравенств Харди и изучила их в терминах более сложных математических объектов - однородных топологических групп.
Набор элементов называется топологической группой, если он одновременно является топологическим пространством и группой, а операции вывода произведения и обратного элемента непрерывны. В топологическом пространстве найдена система подмножеств (топология) специальных свойств. Помимо самих подмножеств топология включает в себя их агрегаты, состоящие из произвольного числа элементов, а также пересечения (только конечные) и множества пустот. Наличие групповой структуры означает, что для множества задана ассоциативная алгебраическая операция, она содержит так называемую «фигуру одного» (ту, которая имеет свойства 1 при умножении), и все элементы имеют обратные.
Существующие методы установления функциональных неравенств в однородных топологических группах основаны на изучении свойств норм. Нормой в математике является неотрицательная составная функция, отвечающая определенным требованиям. Численный модуль и длина вектора являются простыми примерами норм. Новые методы, предложенные авторами исследования, позволяют работать со случайными нормами, а не строго определенными и фиксированными составными функциями, которые использовались ранее.
Результатом работы команды было получение и установление новых типов неравенств Харди в однородных группах. Особое внимание было уделено анализу в абелевых группах. Абелевость (или коммутативность) выражается в независимости результата групповой операции от порядка элементов. Конкретным случаем коммутативности является хорошо известное правило «перестановка слагаемых суммы не меняет значения суммы». Ученые отмечают, что вновь полученные неравенства могут быть использованы в теории нелинейных дифференциальных уравнений.
Результаты исследования в основном теоретические и фундаментальные. Существующие результаты анализа неравенств Харди-типа были пересмотрены и расширены до новых классов математических объектов. Поэтому можно обнаружить еще неизвестные приложения для этих неравенств.
НОВОСТИ
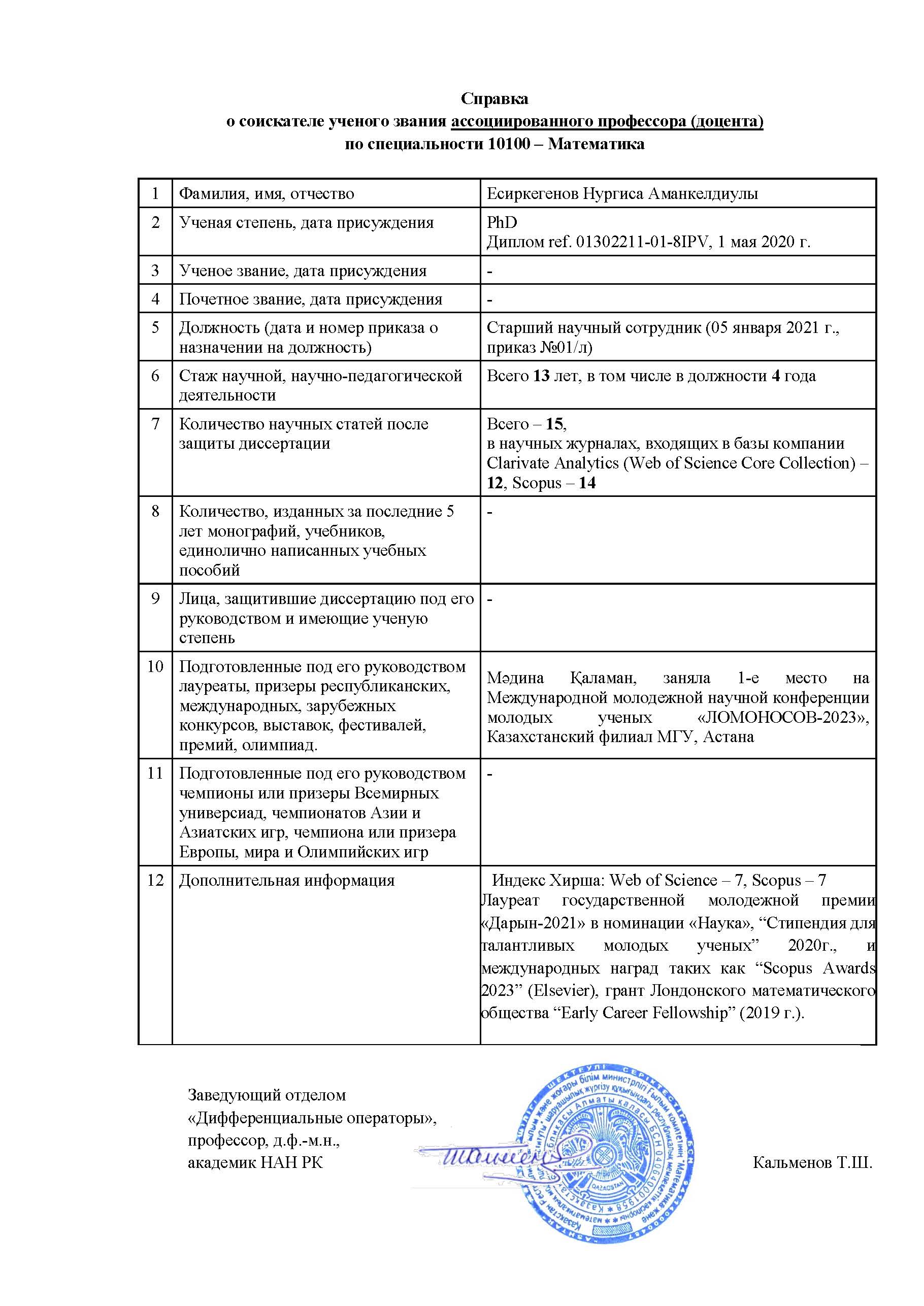
- Документы соискателя ученого звания ассоциированного профессора (доцента) Есиркегенова Нургисы Аманкелдиулы
- “Evolution Equations, Approximation and Spectral Optimization” EEASO-2024
- Документы соискателя ученого звания профессора Кадирбаевой Жазиры Муратбековны
- Документы соискателя ученого звания ассоциированного профессора (доцента) Мынбаевой Сандугаш Табылдиевной
- Информация о Законе "О научно-технической политике"
- ПРОГРАММА И СБОРНИК ТЕЗИСОВ ТРАДИЦИОННОЙ МЕЖДУНАРОДНОЙ АПРЕЛЬСКОЙ НАУЧНОЙ КОНФЕРЕНЦИИ, 16-19 и 22 апреля, 2024
- Второе информационное сообщение, 16-19 апреля, 2024
- Документы соискателя ученого звания ассоциированного профессора (доцента) Сабитбек Болыс Мажитовича
- Первое информационное сообщение, 16-19 апреля, 2024
- Объявление о конкурсе на грантовое финансирование на 2024-2026 годы
- Документы соискателя ученого звания ассоциированного профессора (доцента) Касымова Айдына Адиловича
- Документы соискателя ученого звания профессора Токмагамбетова Нияза Есенжоловича
- Программа отчетной конференции по проекту "Фундаментальные исследования по математике и математическому моделированию"
- Институт математики и математического моделирования поздравляет академика С. Н. Харина с 85-летним юбилеем.
- Международный научный семинар, посвященный 50-летию Виктора Вербовского
- Документы соискателя ученого звания ассоциированного профессора (доцента) Утешовой Розы Есеновны
- ПРОГРАММА И СБОРНИК ТЕЗИСОВ ТРАДИЦИОННОЙ МЕЖДУНАРОДНОЙ АПРЕЛЬСКОЙ НАУЧНОЙ КОНФЕРЕНЦИИ, 5-7 апреля, 2023
- Второе информационное сообщение, 5-7 апреля, 2023
- Первое информационное сообщение, 5-7 апреля, 2023
- Онлайн-собрание по поводу поздравления мужчин, 2022